Statistics of Breath Testing
Yesterday there were some news reports about the opposition party in Victoria issuing a FOI request and finding that the breath testers used to test blood alcohol content routinely under report the readings by up to 20%. They used this fact to show that it was giving negative readings for some people who are a little over the limit. On the face of it this sounds like a problem, but when you look at the statistics the automatic reduction makes sense.
The main point is that breathalyzer tests are not completely accurate. Let's consider the case where the breathalyzer which does no adjustments gives a 0.05 BAC reading. We'd expect the probability distribution for the real BAC reading to be a normal distribution with 0.05 BAC as the mean:
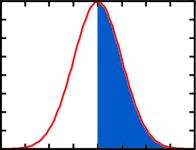
So the real BAC may be either above or below 0.05. Given that it is only an offence to have a BAC above 0.05, the test would only give even odds that the person had broken the law. That would make it pretty useless for getting a conviction.
If you automatically reduce the displayed reading on the breathalyzer by 2 standard deviations, there is a different picture. For a BAC reading of 0.05, the real BAC will still be normally distributed but the mean will be offset:
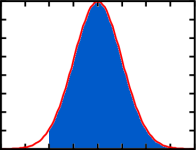
So this gives a 97.5% probability that the BAC is above 0.05. So while removing the automatic result reduction might catch more people over the 0.05 limit, it would also drastically increase the number of people caught while below the limit.
To reduce the number of false negatives without increasing the false positives, the real answer is to use a more accurate test so that the error margins are lower.
Comments:
Johannes -
Hi!
Just for your notice. In Germany breath tests are only used for a fast investigation. You can only be judged if a blood test also gives a positive result. And of course, if people are slightly below the limit in the breath test, they do a blood test, too!
Regards, Johannes
Olaf -
Hi James,
assuming the device is unbiased (something that can easily be fixed if it where so by calibartion) you don't really need a more accurate method. All you need to to is average over several measurements. The mean of n measurements will again be normaly distributed, but with a variance of 1/n*sigma^2 if the original measurements had a variance of sigma^2. So by simply repeating the procedure you get a much lower margin of error.
-- Olaf